Beispiel: Vibrationsminderung durch einen Tilger 

Es ist möglich, Vibrationen in einer Struktur durch zusätzliche strukturdynamische Maßnahmen, wie zum Beispiel Tilger, zu mindern. Hierbei wird die Amplitude einer strukturellen Resonanz reduziert. Als Beispiel dient das in Abbildung 1 (siehe Beispiel Maschinenlagerung) erläuterte Beispiel. Die Vereinfachung dieser Struktur ist in Abbildung 12 zu sehen. Hierbei wird Position 1 der Anregung und Position 2 des Tilgers kollokiert angenommen.

 

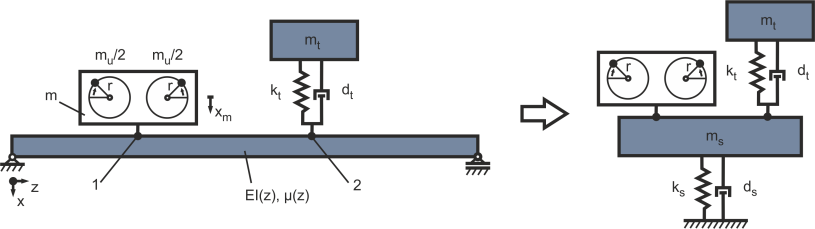
Implementierung in Simulink^®:
Für einen signifikanten Reduktionseffekt ist eine bestimmte Masse des Tilgers erforderlich. Hierbei wird angenommen, dass die Tilgermasse ca. 5 % bis 20 % der Masse der Grundstruktur haben soll [5]. Daher wird für die verwendete Tilgermasse ein Wert von m_t = 100 kg angenommen. Die Steifigkeit ergibt sich in Bezug auf die dominante Resonanzfrequenz der Struktur gekoppelt mit der Maschine von f₁ = 16.5 Hz. Somit ergibt sich eine Steifigkeit von k_t=(f₁ 2π)^2 * m_t = 1.0748e06 N/m für den Tilger.

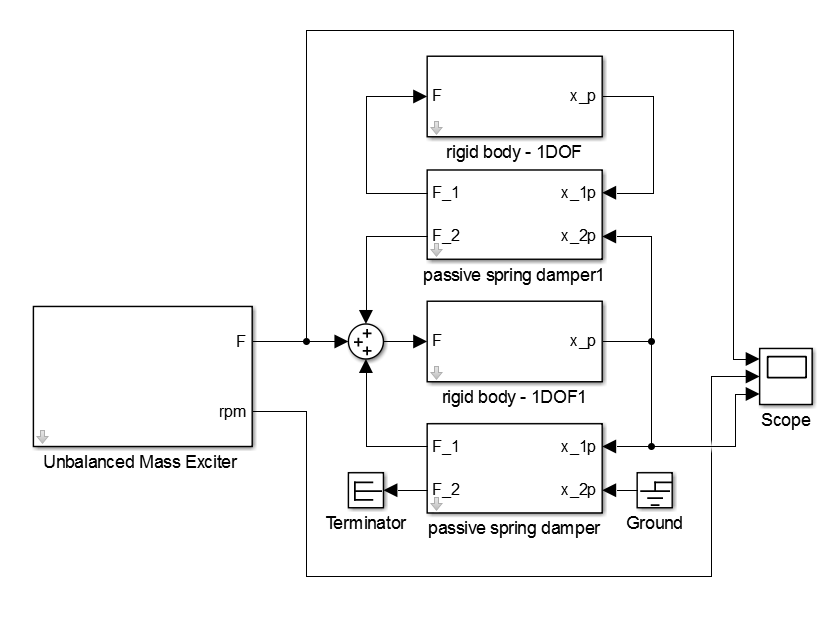
Das Simulationsmodell des Ein-Massen-Schwingers mit dem Tilger in Simulink ist in Abbildung 13 zu sehen. Für die Parametrisierung werden die Eigenschaften aus Tabelle 1 verwendet. Als Dämpfung des Tilgers werden die Werte 1000 kg*s und 4000 kg*s verwendet, welche einen Dämpfungsfaktor von 5% und 20% widerspiegeln.

Ergebnisse:
Der Frequenzbereich wird mit der ma_frequency_response Funktion ausgewertet:

[FREQ,AMPL,PHAS]=ma_frequency_response(ScopeData.time, ScopeData.signals(1).values,
ScopeData.signals(3).values,{0,50});
[FREQ_Damping,AMPL_Damping,PHAS_Damping]=ma_frequency_response(ScopeData_Damping.time,
ScopeData_Damping.signals(1).values, ScopeData_Damping.signals(3).values,{0,50});

figure
semilogy(FREQ,AMPL,’k‘,’LineWidth‘,2); hold on;
semilogy(FREQ_Damping,AMPL_Damping,’r‘,’LineWidth‘,2);
hold off;
grid on
xlabel(‚Frequency in Hz‘)
ylabel(‚Amplitude in m/N‘)
legend(‚Stiff coupling‘,’Mass-damper (\xi50%)‘,’Location‘,’SouthWest‘)
xlim([5 50])

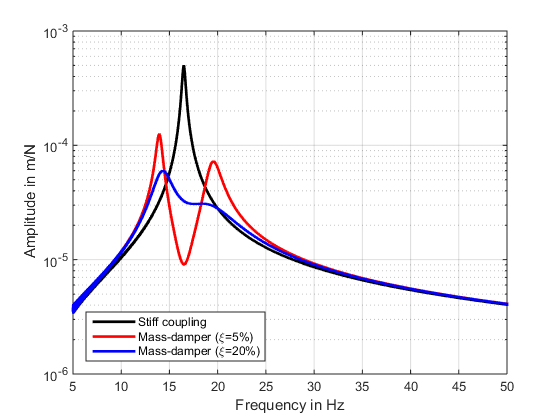
Abbildung 14: Ergebnisse der Reduktionswirkung durch einen Tilger mit einem Dämpfungsfaktor von 5 % und 20 % im Frequenzbereich

In Abbildung 14 werden die Ergebnisse der Reduktionswirkung eines Tilgers mit 5 % und 20 % miteinander im Frequenzbereich verglichen. Für das leicht gedämpfte System wird die Resonanz gedämpft, wobei zwei Nachbarresonanzen entstehen. Diese resultieren aus dem zusätzlich in das System eingebrachten Freiheitsgrad. Für die höhere Dämpfung ist die Amplitude der Nachbarresonanzen geringer, wobei die Effizienz der Reduktionswirkung in der Auslegungsfrequenz ebenfalls abnimmt. Für einen Vergleich der Ergebnisse mit der analytischen Lösung werden die Systemmatrizen mit der Funktion ma_MOSys abgeleitet:

% jData definition of sys1
jData = [1 882.6;
2 100];

% kData definition of sys1
kData = [1 inf 9470328 2000;
1 2 1.0748e6 1000];

% originF definition
originFvalue = 1;

% outputP definition
outputPvalue = 1;

Sys1 = ma_MOSys(jData,kData,’originF‘,originFvalue,’outputP‘,outputPvalue);

Hierbei wird das System in den Zustandsraum überführt und die Eigenwerte berechnet:

ss = ma_MOSysGetSS(Sys1);
eig(ss)

Für die Eigenwerte ergeben sich Frequenzen von 19.47 Hz und 13.96 Hz, welche sich mit den Ergebnissen aus Simulink decken. Für einen Abgleich des Amplitudengangs werden die Transferfunktionen gebildet:

freq_analytic=1:0.1:50;
[mag_analytic, phase_analytic]=bode(ss,freq*2*pi);
mag_analytic=reshape(mag_analytic,1,length(freq));

[FREQ_Damping,AMPL_Damping,PHAS_Damping]=ma_frequency_response(ScopeData_Damping.time,
ScopeData_Damping.signals(1).values, ScopeData_Damping.signals(3).values,{0,50});

figure
semilogy(FREQ_Damping,AMPL_Damping,’k‘,’LineWidth‘,2); hold on;
semilogy(freq_analytic,mag_analytic,’r‘,’LineWidth‘,2);
hold off;
grid on
xlabel(‚Frequency in Hz‘)
ylabel(‚Amplitude in m/N‘)
legend(‚Simulink‘,’analytic‘,’Location‘,’SouthWest‘)
xlim([5 50])

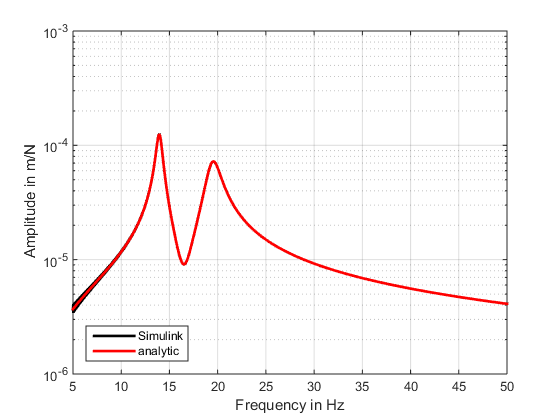Abbildung 15: Abgleich des Simulink-Modells mit der analytischen Lösung

In Abbildung 15 ist deutlich zu erkennen, dass die Ergebnisse aus der Simulation in Simulink und die Lösung des analytischen Modells sehr gut übereinstimmen.