Beispiel: Passive Schwingungsreduktion einer Struktur

Passive Maßnahmen zur Minderung von Vibrationen:
Durch die Verwendung von elastischen Lagern ist es möglich die dynamischen Kräfte, welche durch eine Maschine in eine Struktur eingeleitet werden, zu reduzieren. Als Beispiel soll an dieser Stelle der Aufbau aus Abbildung 1 (siehe Beispiel Maschinenlagerung) dienen. Neben dem dynamischen Verhalten der Maschine muss hierbei ebenso die Charakteristik der Grundstruktur, wie in diesem Fall das Schiff, berücksichtigt werden. Im Allgemeinen werden zwei Anwendungsfälle betrachtet, die Anpassung einer elastischen Lagerung in Bezug auf das Interaktionsverhalten von Maschine und Struktur und die Verwendung von strukturdynamischen Minderungsmaßnahmen.

 

Passive Isolation durch elastische Lagerstellen:
Zu Beginn werden die übertragenen Vibrationen durch eine elastische Lagerung des Motors gemindert. Im Falle einer starren Lagerung in Abbildung 2 (siehe Beispiel Maschinenlagerung) sind die Verschiebungen der Struktur und des Motors xm identisch. Für eine Isolation ist die optimale Wahl der Steifigkeit ki und Dämpfung di besonders wichtig (siehe Abbildung 7). Hierbei setzt die Isolationswirkung oberhalb der Isolationsfrequenz (fz = √2 fo) ein. Zur Beschreibung des Isolationseffektes kann das System zunächst idealisiert betrachtet werden. In diesem Fall kann die Transmission in Abhängigkeit des in Abbildung 7 zu sehenden Systems berechnet werden mit T(s=iω)=x2/x1 =(1+[2ξs/ωi])/(1+[2ξs/ωi]+s²/[ω1]^2 ) [4].

 

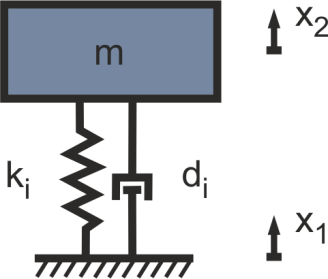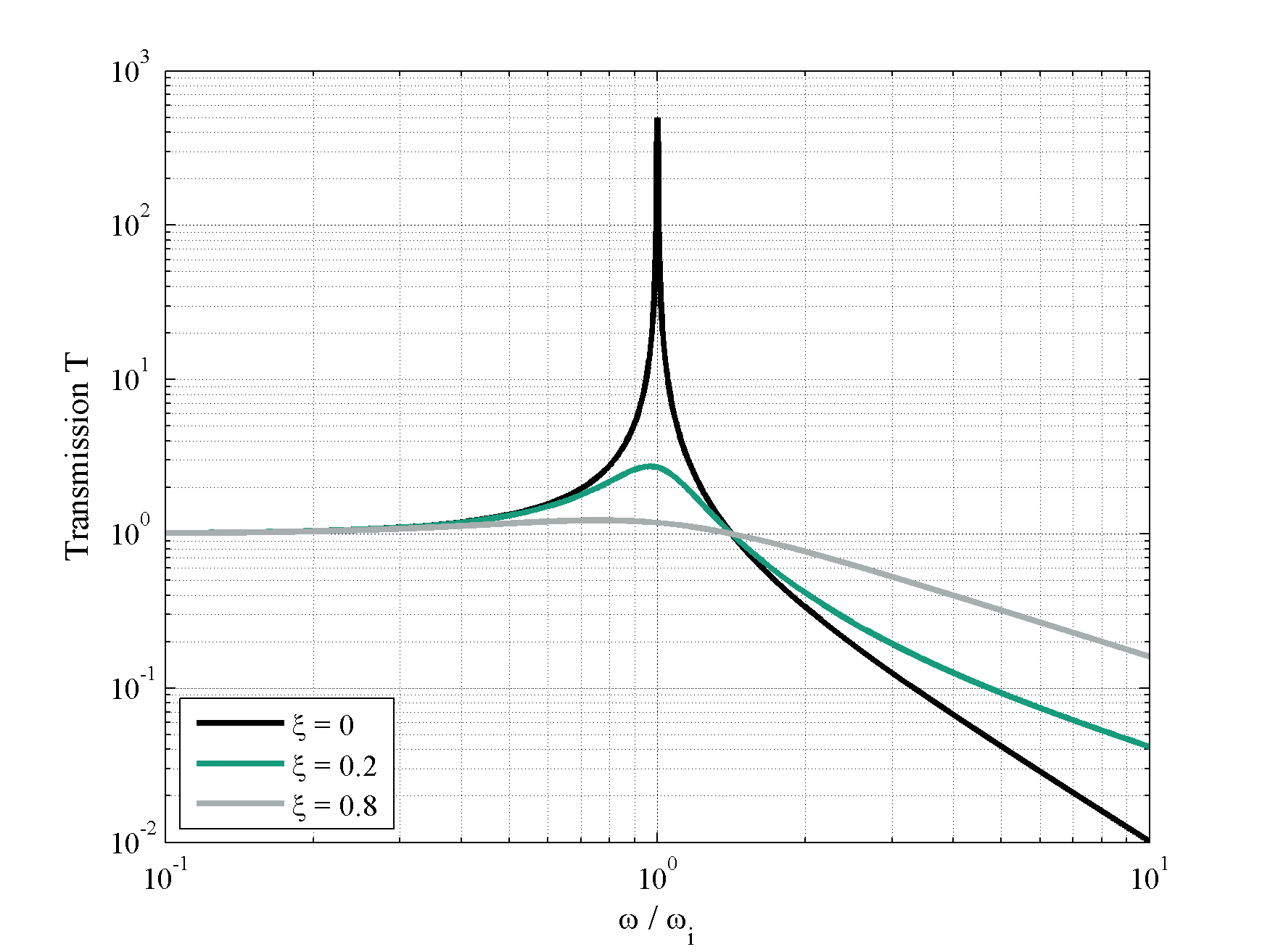Abbildung 7: a) Mechanischer Aufbau eines Isolators b) berechnete Transmission

In Abbildung 7 ist die Transmission der Isolation in Abhängigkeit des Dämpfungsfaktors zu sehen. Für den ungedämpften Fall (ξ=0) geht die Amplitude in der Resonanz gegen unendlich. Oberhalb der Isolationsfrequenz fällt die Transmission mit einem Wert von 40 dB/Dekade ab. Durch eine Steigerung der Dämpfung ist es möglich die Amplitude an der Stelle der Resonanz zu mindern. Gleichzeit wird jedoch auch der Isolationseffekt reduziert.

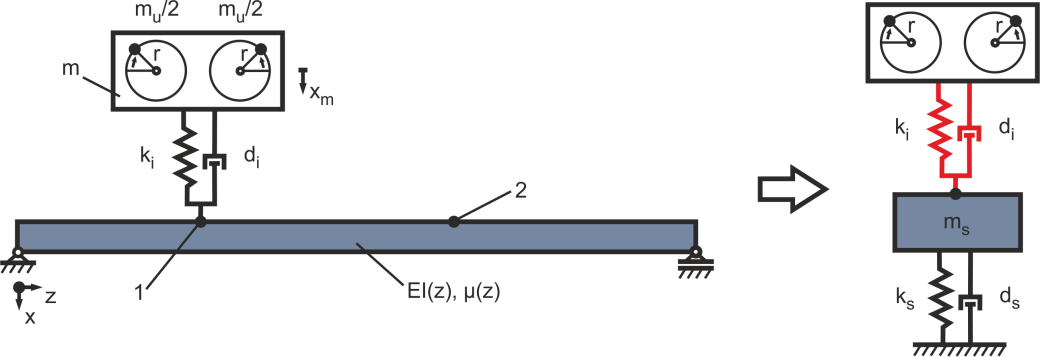
Abbildung 8: Vereinfachung der Struktur mit einer elastischen Lagerung der Anregung

Die Steifigkeit der Isolation ki muss unter Berücksichtigung der Masse der Maschine m gewählt werden. Hierbei ist es wichtig den Isolationsbereich so zu gestalten, dass er den Betriebsdrehzahlbereich nu=30ωu/π abdeckt (ωu>ωi ). Die Isolationsfrequenz kann bezüglich der Resonanzfrequenz berechnet werden. Dies wird bedingt durch die Steifigkeit ki und die Masse m, unter der Annahme, dass ki < k1 (Steifigkeit der Struktur an der Anbindungsposition) mit ωi^2≈(2k_i)/m [1]. Nimmt man als untere Drehzahlgrenze 1200 rpm für eine Maschine der Masse m = 600 kg, muss die Steifigkeit unter einem Wert von ki < 2.1e6 N/m liegen. In diesem Fall wird ein Wert von  ki = 2e6 N/m angenommen. Für diese Konfiguration ergibt sich eine Isolationsfrequenz von fi=√(ki/m)/(2π)=9.2 Hz . Die Dämpfung der Isolation di ist wichtig für die Begrenzung der Amplitude der Resonanzfrequenz für den Fall, dass die Anregung bei einem Hochlauf hindurchfährt. Auf der anderen Seite ist es wichtig die Dämpfung im Hinblick auf  die Isolationswirkung nicht zu hoch zu wählen. Aus diesem Grund wird eine Dämpfung von di = 1000 kg*s angenommen.

 

Implementierung in Simulink:®

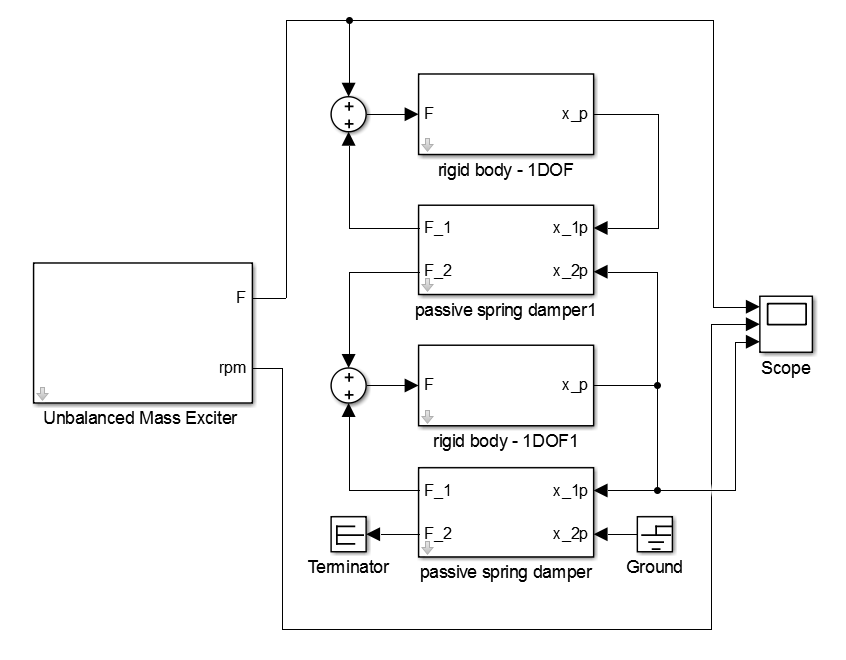
Abbildung 9: Simulink Block-Diagramm des gedämpften Ein-Massen-Schwingers mit isolierter Anregung
 
 

Für Simulationen im Zeitbereich wird ein Simulink-Modell erstellt (siehe Abbildung 9). Für die Parametrisierung werden die Eigenschaften aus Tabelle 1 verwendet.

Ergebnisse:
In Abbildung 10 sind die Ergebnisse im Zeit- und Frequenzbereich zu sehen. Der Frequenzbereich wird mit der ma_frequency_response Funktion ausgewertet:

[FREQ,AMPL,PHAS]=ma_frequency_response(ScopeData.time, ScopeData.signals(1).values,
ScopeData.signals(3).values,{0,50});

[FREQ_Isolation,AMPL_Isolation,PHAS_Isolation]=ma_frequency_response(ScopeData_Isolation.time, ScopeData_Isolation.signals(1).values, ScopeData_Isolation.signals(3).values,{0,50});

figure

semilogy(FREQ,AMPL,’k‘,’LineWidth‘,2); hold on;

semilogy(FREQ_Isolation,AMPL_Isolation,’r‘,’LineWidth‘,2);

hold off;

grid on

xlabel(‚Frequency in Hz‘)

ylabel(‚Amplitude in m/N‘)

legend(’stiff coupling‘,’isolation‘,’Location‘,’SouthWest‘)

xlim([5 50])

Für das starr verkoppelte System kann deutlich die Resonanz bei 16.5 Hz erkannt werden. Im Fall des isolierten Systems entsteht eine zusätzliche Resonanz bei 8.3 Hz, welche unterhalb des Betriebsbereichs liegt. Die Hauptresonanz der Grundstruktur verschiebt sich zu 32.3 Hz. Somit liegt sie immer noch im Betriebsbereich der Anregung, jedoch mit einer deutlich geringeren Amplitude.

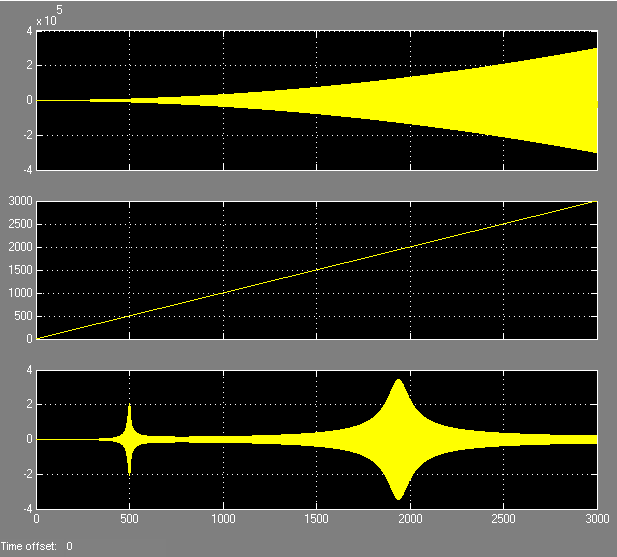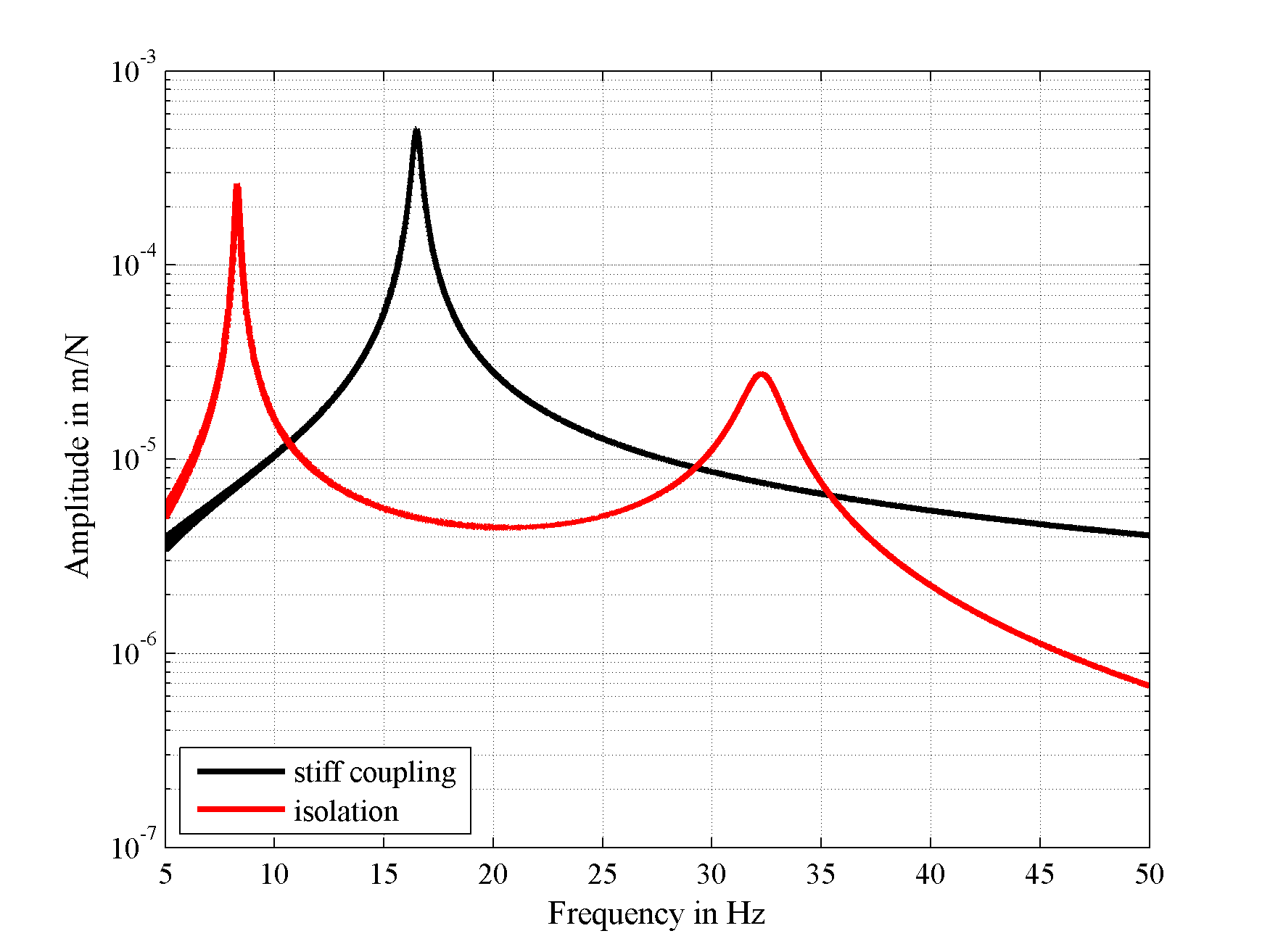Abbildung 10: Ergebnisse im a) Zeit- und b) Frequenzbereich

Für einen Vergleich der Ergebnisse mit der analytischen Lösung werden die Systemmatrizen mit der Funktion ma_MOSys abgeleitet:

% jData definition of sys1

jData = [1 282.6;

2 600];

% kData definition of sys1

kData = [1 inf 9470328 2000;

1 2   2e6     1000];

% Sys1 = ma_MOSys(jData,kData)

% originF definition

originFvalue = 2;

% outputP definition

outputPvalue = 1;

Sys1 = ma_MOSys(jData,kData,’originF‘,originFvalue,’outputP‘,outputPvalue);

Hierbei wird das System in den Zustandsraum überführt und die Eigenwerte berechnet:

ss = ma_MOSysGetSS(Sys1);

eig(ss)

Für die Eigenwerte ergeben sich Frequenzen von 8.29 Hz und 32.3 Hz, welche sich mit den Ergebnissen aus Simulink decken. Für einen Abgleich des Amplitudengangs werden die Transferfunktionen gebildet:

freq_analytic=1:0.1:50;

[mag_analytic, phase_analytic]=bode(ss,freq*2*pi);

mag_analytic=reshape(mag_analytic,1,length(freq));

[FREQ_Isolation,AMPL_Isolation,PHAS_Isolation]=ma_frequency_response(ScopeData_Isolation.time, ScopeData_Isolation.signals(1).values, ScopeData_Isolation.signals(3).values,{0,50});

figure

semilogy(FREQ_Isolation,AMPL_Isolation,’k‘,’LineWidth‘,2); hold on;

semilogy(freq_analytic,mag_analytic,’r‘,’LineWidth‘,2);

hold off;

grid on

xlabel(‚Frequency in Hz‘)

ylabel(‚Amplitude in m/N‘)

legend(‚Simulink‘,’analytic‘,’Location‘,’SouthWest‘)

xlim([5 50])

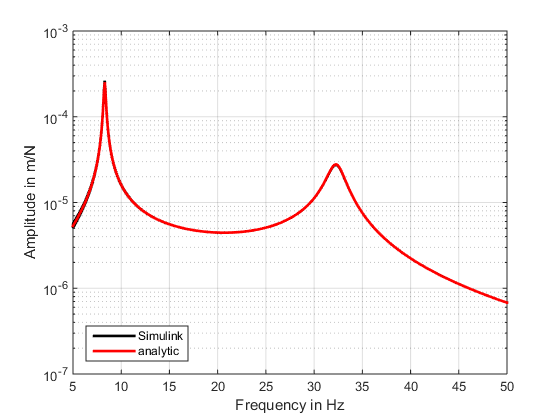
Abbildung 11: Abgleich des Simulink-Modells mit der analytischen Lösung

In Abbildung 11 ist deutlich zu erkennen, dass die Ergebnisse aus der Simulation in Simulink und die Lösung des analytischen Modells sehr gut übereinstimmen.

 

 
Menü schließen