Passive Maßnahmen zur Schwingungsminderung am Beispiel einer Tragwerksstruktur mit gelagerter Maschine :: Tutorial (Fraunhofer LBF) |
 |
Problembeschreibung
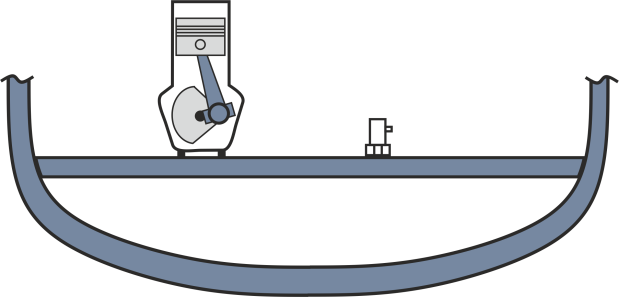
Im Betrieb von Maschinen treten häufig unerwünschte Schwingungen auf. Diese Schwingungen können die Funktion der Maschine beeinträchtigen und im ungünstigsten Fall zu vorzeitigem Materialversagen führen. Darüber hinaus stellen die resultierenden Vibrationen und die damit einhergehende Schallentwicklung eine Belastung für die Umgebung dar. Insbesondere im Resonanzfall, wenn die Anregungsfrequenz mit der Eigenfrequenz des Systems übereinstimmt, führt dies zu einer Verstärkung der resultierenden Schwingungsamplituden. Es ist daher eine wichtige Aufgabe der Maschinendynamik solche unerwünschten Schwingungen durch geeignete konstruktive Maßnahmen zu reduzieren. Die resultierenden Schwingungen beschränken sich nicht auf einzelne Bauteile, sondern auch angrenzende Strukturen werden durch die Wechselwirkungen von Kräften und Bewegungen zu Schwingungen angeregt. Daher ist nicht nur das dynamische Verhalten der Maschine selbst zu betrachten, auch die Eigenschaften des Aufstellungsortes – insbesondere der Lagerstellen – haben einen großen Einfluss auf das Schwingungsverhalten des Gesamtsystems. Die AdaptroSim Toolbox stellt Inhalte für Matlab und Simulink zur Verfügung, mit denen das dynamische Verhalten modelliert und der Einfluss konstruktiver Maßnahmen auf dieses Verhalten untersucht werden kann. Im Folgenden wird die Vorgehensweise am Beispiel eines Verbrennungsmotors in einem Schiffsrumpf gezeigt (siehe Abbildung 1). Dazu wird das reale System in ein geeignetes Modell überführt und das dynamische Verhalten des Gesamtsystems simuliert. Der Motor wird zunächst als fest mit der elastischen Struktur des Aufstellungsortes verbunden betrachtet und der Einfluss der maschineninduzierten Schwingungen an diesem Modell ermittelt. Anschließend werden mögliche passive Verfahren zur Schwingungsreduktion (Schwingungsisolation durch Optimierung der Lagerstellen, Schwingungstilgung durch eine geeignete Zusatzmasse) untersucht und das mechanische System um entsprechende Komponenten erweitert.
Mechanisches Ersatzsystem
Reale Strukturen weisen häufig einen hohen Grad an Komplexität auf. Aus diesem Grund ist es sinnvoll grundlegende Untersuchungen an vereinfachten Strukturen durchzuführen. Dazu wird das reale System in ein mechanisches Ersatzsystem überführt. Dieses muss die zu untersuchenden Eigenschaften des realen Systems hinreichend genau wiedergeben.
Als Motor wird ein 12-Zylindermotor mit einem Gesamtgewicht von 600 kg angenommen. Jeder Zylinder hat eine Masse von 16 kg bei einem Hub von 190 mm. Der typische Frequenzbereich liegt bei 13 – 34 Hz was einer Drehzahl von 800 – 2000 rpm entspricht. Der idealisierte Motor kann als Unwuchterreger mit der Gesamtmasse mm, der Drehfrequenz Ω und der Unwuchtmasse mu, die sich um den Radius r bewegt, abgebildet werden. Die resultierende Kraft des Unwuchterregers ergibt sich zu 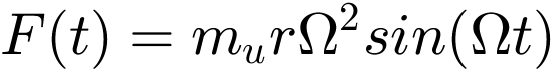 . Der Schiffsboden wird im einfachsten Fall als gelenkig gelagerter Balken mit dem Elastizitätsmodul E, dem Flächenträgheitsmoment I und der längenbezogenen Masse μ modelliert. Dieser Balken kann in ein äquivalentes Feder-Masse-Dämpfer-System mit einem Freiheitsgrad überführt werden. Dazu werden zunächst die Schwingungseigenschaften des Balkens berechnet und anschließend die Parameter des Feder-Masse-Dämpfer-Systems (ms, ks und ds) so bestimmt, dass sie das Schwingungsverhalten des Systems an einer bestimmten Position wiedergeben. Im Folgenden wird vereinfachend davon ausgegangen, dass der Motor in der Mitte des Balkens angeordnet ist (Position 1, z = L/2) und diese Position mit der Position, an der die Bewegung der Struktur
. Der Schiffsboden wird im einfachsten Fall als gelenkig gelagerter Balken mit dem Elastizitätsmodul E, dem Flächenträgheitsmoment I und der längenbezogenen Masse μ modelliert. Dieser Balken kann in ein äquivalentes Feder-Masse-Dämpfer-System mit einem Freiheitsgrad überführt werden. Dazu werden zunächst die Schwingungseigenschaften des Balkens berechnet und anschließend die Parameter des Feder-Masse-Dämpfer-Systems (ms, ks und ds) so bestimmt, dass sie das Schwingungsverhalten des Systems an einer bestimmten Position wiedergeben. Im Folgenden wird vereinfachend davon ausgegangen, dass der Motor in der Mitte des Balkens angeordnet ist (Position 1, z = L/2) und diese Position mit der Position, an der die Bewegung der Struktur ![]() gemessen wird (Position 2), übereinstimmt (siehe Abbildung 2). [1]
gemessen wird (Position 2), übereinstimmt (siehe Abbildung 2). [1]
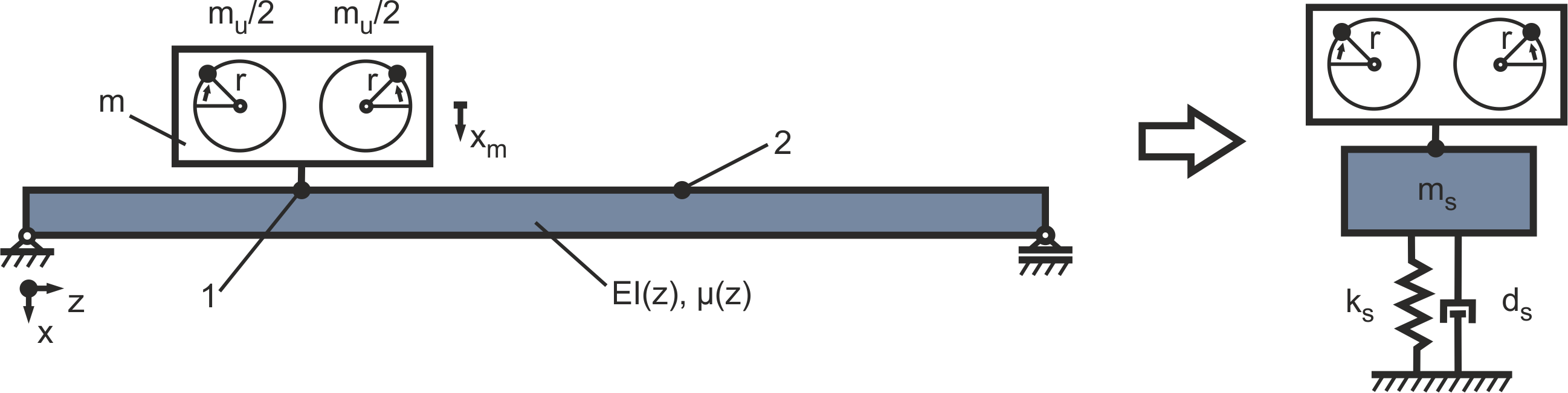
Abbildung 2: Mechanisches Ersatzsystem der Struktur als gelenkig gelagerter Balken und äquivalentes Masse-Feder-Dämpfer-System mit einem Freiheitsgrad
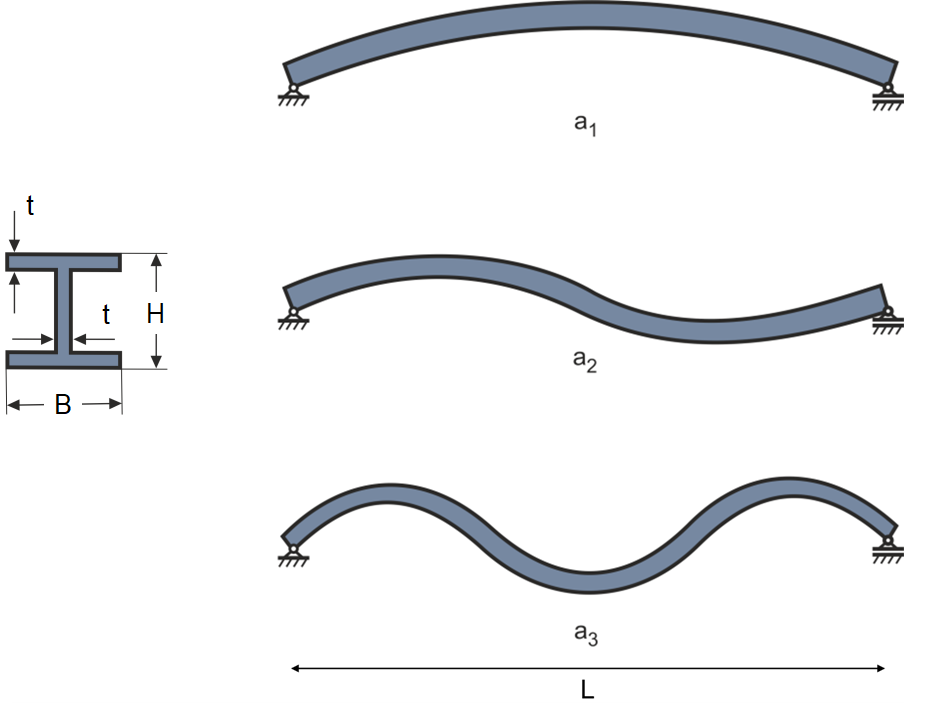
Schwingungseigenschaften des Balkens: Für die Geometrie des Balkens wird ein I-Profil mit den Abmessungen H = 0.2 m, B = 0.2 m, t = 0.02 m und einer Länge L = 4.8 m gewählt (Abbildung 3). Als Werkstoff wird Stahl mit einem Elastizitätsmodul von E = 2.1e+11 N/m2 und einer Dichte von ρ = 7850 kg/m3 angenommen. Mit diesen Werten kann das Flächenträgheitsmoment mit 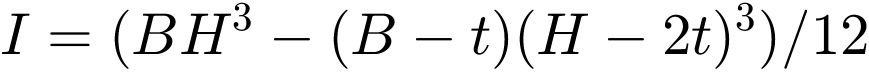 = 7.1893e-05 m4 und die Querschnittsfläche
= 7.1893e-05 m4 und die Querschnittsfläche 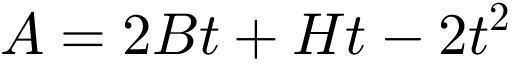 = 0.0112 m2 berechnet werden. [2] Mit der längenbezogenen Masse μ = ρA = 87.92 kg/m ergeben sich unter der Annahme einer vernachlässigbar geringen Dämpfung die ersten drei Eigenfrequenzen aus
= 0.0112 m2 berechnet werden. [2] Mit der längenbezogenen Masse μ = ρA = 87.92 kg/m ergeben sich unter der Annahme einer vernachlässigbar geringen Dämpfung die ersten drei Eigenfrequenzen aus
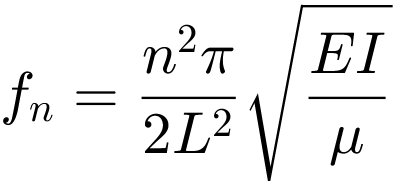
mit n = 1, 2, 3 zu f1 = 28.252 Hz, f2 = 113.01 Hz und f3 = 254.27 Hz. Abbildung 3 zeigt die zugehörigen Eigenmoden a1, a2 und a3. Die erste Resonanzfrequenz der Grundstruktur ist im Folgenden von besonderem Interesse, da sie im betrachteten Frequenzbereich des Motors liegt.
Um einen äquivalenten Einmassenschwinger zu erhalten, werden unter Berücksichtigung der Biegeform sowie der potentiellen und kinetischen Energie eine äquivalente Masse und eine äquivalente Steifigkeit berechnet. Die äquivalente Masse
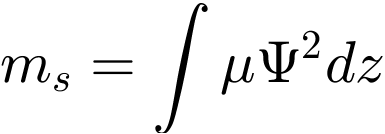
ergibt sich für die in Abbildung 3 dargestellte sinusförmige Eigenform 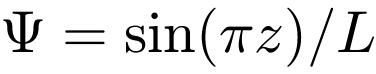 an der Stelle
an der Stelle 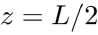 zu
zu 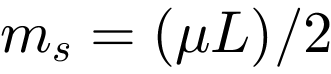 = 211.01 kg. Unter Berücksichtigung der konzentrierten Gesamtmasse des Motors mm beträgt die äquivalente Gesamtmasse
= 211.01 kg. Unter Berücksichtigung der konzentrierten Gesamtmasse des Motors mm beträgt die äquivalente Gesamtmasse  = 811.01 kg. Die äquivalente Steifigkeit beträgt
= 811.01 kg. Die äquivalente Steifigkeit beträgt 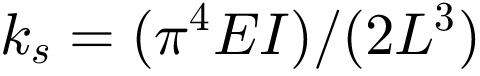 = 6.649e+06 N/m. Als Dämpfung der Struktur wird eine hysteretische Dämpfung von etwa η = 4% angenommen. Die äquivalente modale Dämpfung ergibt sich damit zu
= 6.649e+06 N/m. Als Dämpfung der Struktur wird eine hysteretische Dämpfung von etwa η = 4% angenommen. Die äquivalente modale Dämpfung ergibt sich damit zu 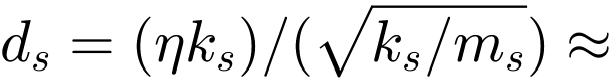 1000 kg/s.[3]
1000 kg/s.[3]
Implementierung in Simulink
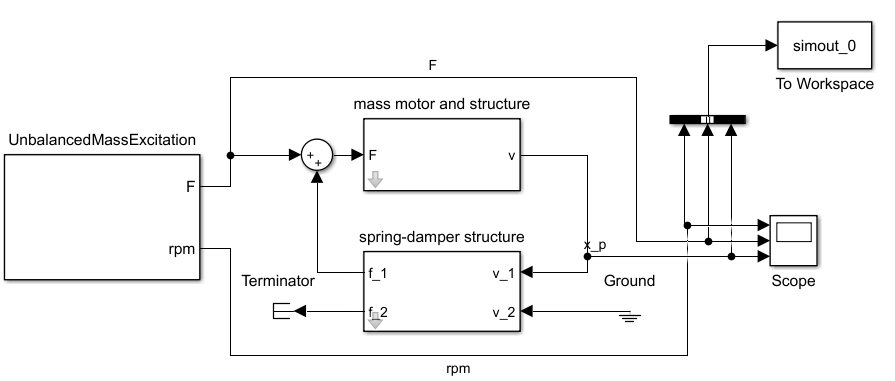
Abbildung 4: Simulink Model des gedämpften Ein-Massen-Schwingers
Die Zeitbereichssimulationen werden mit Simulink durchgeführt. Dazu wird das in Abbildung 4 dargestellte Modell erstellt, wobei die Simulationen mit dem Fixed-step Solver und einer festen Samplingrate von ts = 0.001 s für eine Zeit von 0 bis t_end = 30 s durchgeführt werden. Zur Implementierung des Modells werden die Blöcke Stiffness1DOF, RigidBody1DOF und UnbalancedMassExcitation aus der „Structure and Vibration“ Toolbox verwendet. Diese werden mit den zuvor ermittelten Werten parametrisiert. Für den Unwuchterreger wird ein Drehzahlbereich von 0 bis 3000 rpm und einer Beschleunigungsrate von 100 1/min/s gewählt. Die Parameter der Blöcke sind in Tabelle 1 zusammengefasst:
Tabelle 1. Parametrisierung des Modells
| BlockName | BlockType | BlockProperty | VariableName | PropertValue |
|---|---|---|---|---|
| Masse Motor und Struktur | RigidBody1DOF | inertia (weight of the mass [kg] or moment of inertia [kgm^2]) | m_ges | 811.01 |
| Feder-Dämpfer Struktur | Stiffness1DOF | stiffness [N/m] | k_s | 6.649e+06 |
| damping coefficient [Ns/m] | d_s | 1000 | ||
| UnbalancedMassExcitation | UnbalancedMassExcitation | unbalanced mass [kg] | m_u | 16 |
| eccentricity of the unbalance [m] | r_u | 0.19 | ||
| idle speed [1/min] | rpm0 | 0 | ||
| speed ratio at start-up [1/min/s] | rpm_ratio | 100 | ||
| sample time [s] | ts | 0.001 |
Zur Weiterverarbeitung der Daten außerhalb von Simulink werden die Signale mit Hilfe des Simulink To Workspace Blocks als „Structure with Time“ exportiert (simout_0). Abbildung 5 zeigt die Ergebnisse der Simulation im Zeitbereich. Die oberen beiden Achsen zeigen die Drehzahl des Motors sowie die aus der Unwucht resultierende Kraft. Die untere Achse gibt die Geschwindigkeit des Balkens an der Position 1 wieder. Es ist deutlich erkennbar, dass diese nach etwa 9 Sekunden stark ansteigt. Dies ist auf die direkte Kopplung der Maschinenmasse und des Balkens zurückzuführen.
▾ Show source code
% Display simulation data in time domain time_0 = simout_0.time; rpm_0 = simout_0.signals.values(:,1); F_0 = simout_0.signals.values(:,2); x_0 = simout_0.signals.values(:,3); h = figure(); subplot(3,1,1); title('Simulation result - Time domain') ma_graphics.plot(time_0,rpm_0); ylabel('rpm'); subplot(3,1,2); ma_graphics.plot(time_0,F_0); ylabel('F'); subplot(3,1,3); ma_graphics.plot(time_0,x_0); ylabel('$\dot{x}$','Interpreter','latex','FontSize',15); xlabel('time'); ylim([-13,13]); ah = findobj(h,'type','axes'); set(ah,'XGrid','on','YGrid','on');
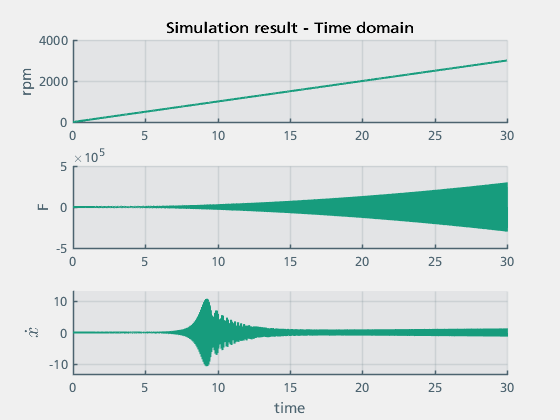
Abbildung 5: Simulationsergebnisse im Zeitbereich
Um die Ergebnisse genauer betrachten zu können, werden im Folgenden die Simulationsergebnisse mit Hilfe der Funktion ma_frequency_response in den Frequenzbereich transformiert.
▾ Show source code
% Display simulation results in frequency domain
ma_frequency_response(time_0, F_0, x_0,{0,50});
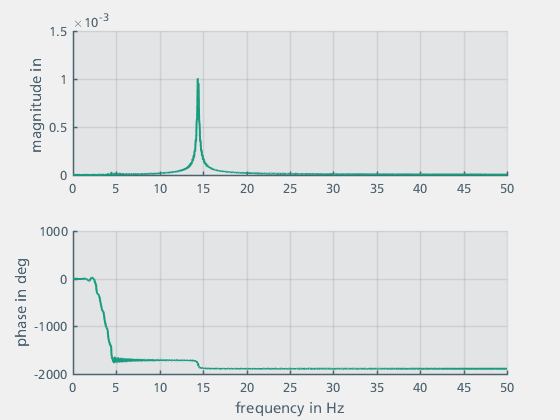
Abbildung 6: Simulationsergebnisse im Frequenzbereich
Die Resonanz bei einer Frequenz von ca. 14 Hz ist deutlich zu erkennen. Die beobachtete Resonanz entspricht dem Ergebnis der analytisch berechneten Eigenfrequenz des Systems 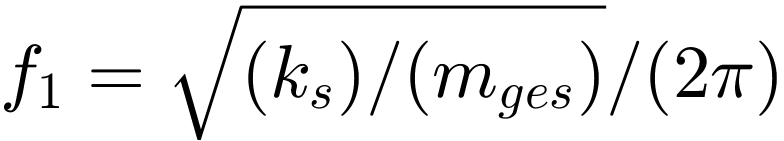 = 14.411 Hz.
= 14.411 Hz.
Passive Isolation durch elastische Lagerstellen
Durch die Verwendung von elastischen Lagern können die dynamischen Kräfte, die von einer Maschine in eine Struktur eingeleitet werden, reduziert werden. Im Folgenden wird die Vorgehensweise anhand des in diesem Tutorial betrachteten Schiffsmotors gezeigt. Neben dem dynamischen Verhalten der Maschine müssen auch die Eigenschaften der Grundstruktur, in diesem Fall des Schiffes, berücksichtigt werden. Bei einer starren Lagerung, wie sie im vorherigen Abschnitt betrachtet wurde, sind die Verschiebungen der Struktur xs und des Motors xm identisch. Durch ein zusätzliches Feder-Dämpfer-Element (ki, di) kann eine Schwingungsisolation erreicht werden. Hierfür ist eine geeignete Wahl der Steifigkeits- und Dämpfungsparamter entscheidend.
Zur Beschreibung der Isolationswirkung wird das System aus Motormasse und Isolator-Feder-Dämpfer zunächst idealisiert betrachtet (siehe Abbildung 7).
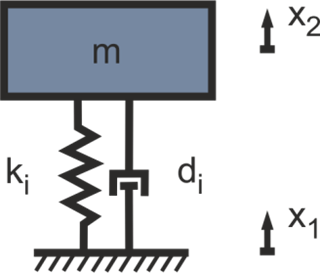
Abbildung 7: Mechanischer Aufbau eines Isolators
Das Übertragungsverhalten des in Abbildung 7 dargestellten Isolators wird durch die Funktion

wiedergegeben. Dabei gilt 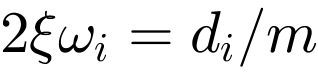 und
und 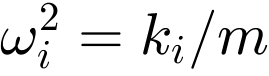 . Die Isolationswirkung setzt oberhalb der effektiven Frequenz
. Die Isolationswirkung setzt oberhalb der effektiven Frequenz 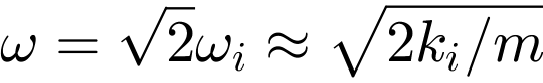 ein.
ein.
Abbildung 8 zeigt das Übertragungsverhalten des Isolators in Abhängigkeit zum Dämpfungsfaktor ξ. Für den ungedämpften Fall (ξ = 0) geht die Amplitude in der Resonanz gegen unendlich. Oberhalb der Isolationsfrequenz fällt die Transmission mit einem Wert von 40 dB/Dekade ab. Durch Erhöhung der Dämpfung wird die Amplitude an der Stelle der Resonanz gemindert wodurch jedoch gleichzeitig der Isolationseffekt reduziert wird.[4]

Abbildung 8: Transmission des Isolators
Um eine Schwingungsisolation durch eine elastische Lagerung des Motors zu modellieren, wird das in Abbildung 2 dargestellte Modell um ein Feder-Dämpfer-Element erweitert (siehe Abbildung 9). Die Steifigkeit der Isolation ki ist unter Berücksichtigung der Maschinenmasse mm = 600 kg zu wählen. Dabei ist es wichtig, ki so zu wählen, dass die Isolationswirkung den Betriebsdrehzahlbereich 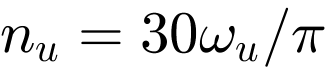 abdeckt. Im konkreten Fall bedeutet dies, dass die Isolationsfrequenz ωi so zu wählen ist, dass die effektive Isolationswirkung (
abdeckt. Im konkreten Fall bedeutet dies, dass die Isolationsfrequenz ωi so zu wählen ist, dass die effektive Isolationswirkung (![]() ) unterhalb der unteren Drehzahlgrenze von 800 rpm bzw. einer Kreisfrequenz von ω = 83.776 Hz einsetzt. Unter der Annahme, dass ki < ks kann die gesuchte Isolationsfrequenz mit
) unterhalb der unteren Drehzahlgrenze von 800 rpm bzw. einer Kreisfrequenz von ω = 83.776 Hz einsetzt. Unter der Annahme, dass ki < ks kann die gesuchte Isolationsfrequenz mit 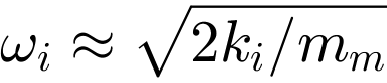 bestimmt werden. Daraus folgt, dass die Steifigkeit kleiner als 2.1055e+06 N/m sein muss. In diesem Beispiel wird ein Wert von 2000000 N/m gewählt. Für diese Konfiguration ergibt sich eine Isolationsfrequenz von
bestimmt werden. Daraus folgt, dass die Steifigkeit kleiner als 2.1055e+06 N/m sein muss. In diesem Beispiel wird ein Wert von 2000000 N/m gewählt. Für diese Konfiguration ergibt sich eine Isolationsfrequenz von 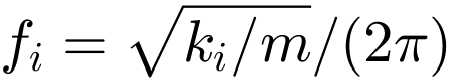 = 9.1888 Hz.
= 9.1888 Hz.
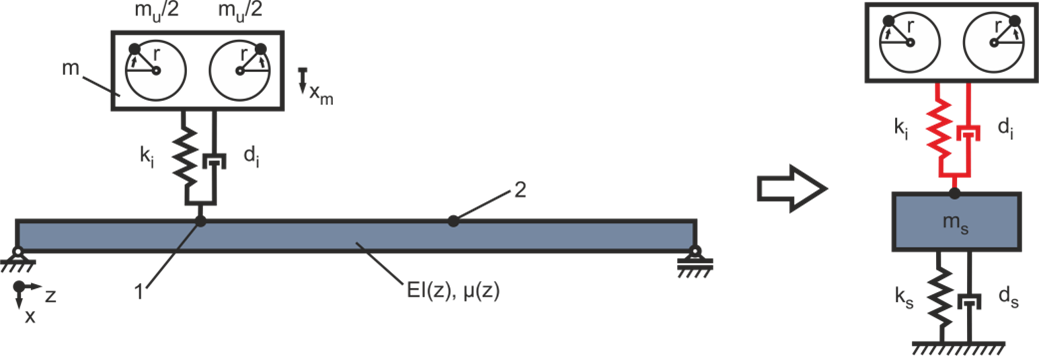
Abbildung 9: Mechanisches Modell mit einer elastischen Lagerung der Anregung
Die Dämpfung der Isolation di ist wichtig um die Amplitude der Resonanzfrequenz zu begrenzen, da die Anregung diese beim Hochlauf hindurchfährt.
Andererseits ist es wichtig die Dämpfung im Hinblick auf die Isolationswirkung nicht zu groß zu wählen. Im Folgenden wird ein Dämpfungsfaktor ζ von ca. 2% angenommen. Daraus ergibt sich mit 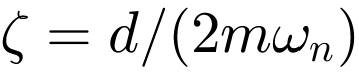 die Dämpfungskonstante des Isolators di. Im vorliegenden Beispiel wird eine Dämpfungskonstante di = 1400 kg*s angenommen.
die Dämpfungskonstante des Isolators di. Im vorliegenden Beispiel wird eine Dämpfungskonstante di = 1400 kg*s angenommen.
Implementierung in Simulink
Abbildung 10 zeigt das um die elastische Lagerung erweiterte Simulink-Modell. Die Modellparameter sind in Tabelle 2 aufgeführt.
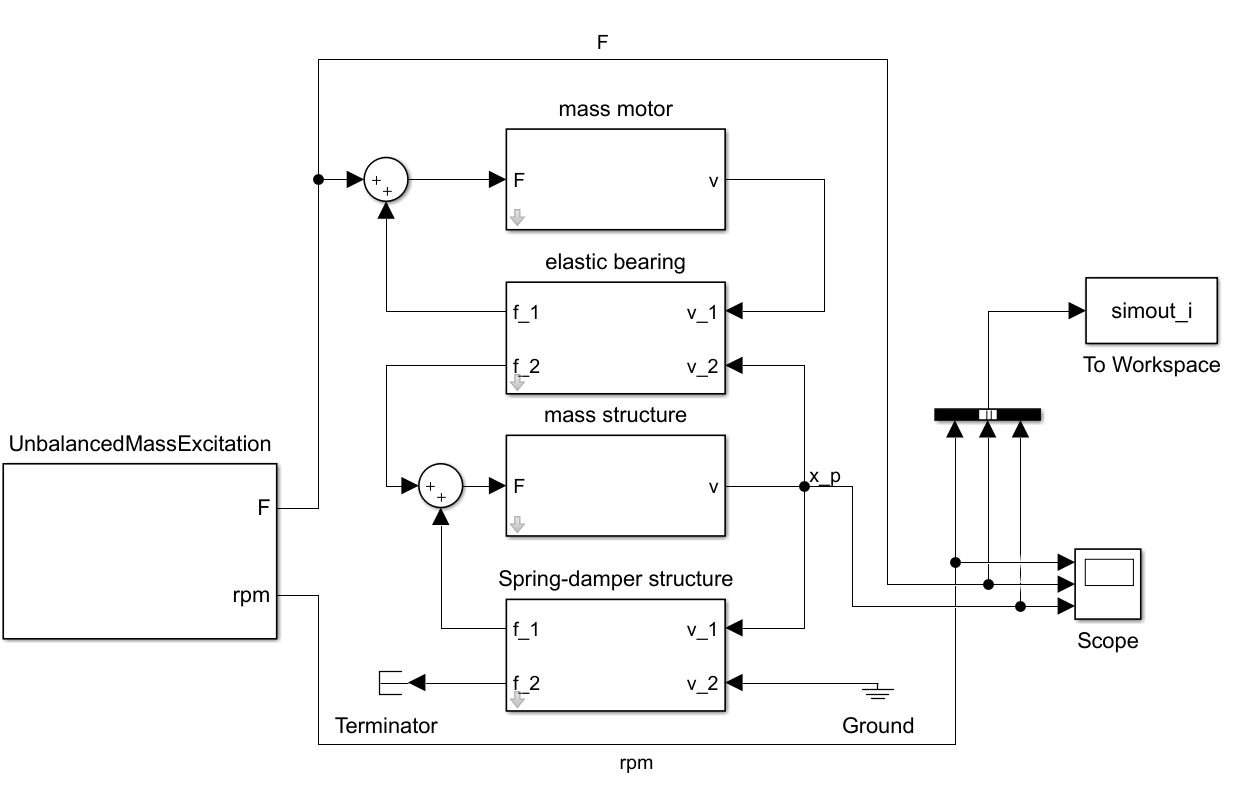
Abbildung 10: Simulink Model des elastisch gelagerten Motors
Tabelle 2. Parametrisierung des Modells
| BlockName | BlockType | BlockProperty | VariableName | PropertValue |
|---|---|---|---|---|
| Masse Motor | RigidBody1DOF | inertia (weight of the mass [kg] or moment of inertia [kgm^2]) | m_m | 600 |
| Masse Struktur | RigidBody1DOF | inertia (weight of the mass [kg] or moment of inertia [kgm^2]) | m_s | 211.01 |
| Feder-Dämpfer Struktur | Stiffness1DOF | stiffness [N/m] | k_s | 6.649e+06 |
| damping coefficient [Ns/m] | d_s | 1000 | ||
| Elastische Lagerung | Stiffness1DOF | stiffness [N/m] | k_i | 2000000 |
| damping coefficient [Ns/m] | d_i | 1400 | ||
| UnbalancedMassExcitation | UnbalancedMassExcitation | unbalanced mass [kg] | m_u | 16 |
| eccentricity of the unbalance [m] | r_u | 0.19 | ||
| idle speed [1/min] | rpm0 | 0 | ||
| speed ratio at start-up [1/min/s] | rpm_ratio | 100 | ||
| sample time [s] | ts | 0.001 |
Die Simulationsergebnisse simout_i werden in Matlab weiter verarbeitet. Abbildung 11 zeigt die Ergebnisse der Simulation im Zeitbereich.
▾ Show source code
% Display simulation data in time domain time_i = simout_i.time; rpm_i = simout_i.signals.values(:,1); F_i = simout_i.signals.values(:,2); x_i = simout_i.signals.values(:,3); h = figure(); subplot(3,1,1); title('Simulation result - Time domain') ma_graphics.plot(time_i,rpm_i); ylabel('rpm'); subplot(3,1,2); ma_graphics.plot(time_i,F_i); ylabel('F'); subplot(3,1,3); ma_graphics.plot(time_i,x_i); ylabel('$\dot{x}$','Interpreter','latex','FontSize',15); xlabel('time'); ylim([-6,6]); ah = findobj(h,'type','axes'); set(ah,'XGrid','on','YGrid','on');

Abbildung 11: Simulationsergebnisse im Zeitbereich
Im Folgenden werden die Ergebnisse im Frequenzbereich betrachtet (Abbildung 12) und die Simulationsergebnisse des elastisch gelagerten Motors mit denen des starr verbundenen Motors verglichen. Durch die elastische Lagerung wurde die Resonanzfrequenz nach 32 Hz verschoben. Diese liegt zwar im Betriebsbereich der Anregung, hat jedoch eine deutlich geringere Amplitude. Bei 8 Hz tritt eine zusätzliche Resonanz auf, die jedoch außerhalb des Betriebsbereiches liegt.
▾ Show source code
% Display simulation results in frequency domain [FREQ_0,AMPL_0,PHAS_0] = ma_frequency_response(time_0, F_0, x_0,{0,50},'window',true); [FREQ_i,AMPL_i,PHAS_i] = ma_frequency_response(time_i, F_i, x_i,{0,50},'window',true); figure(); ma_graphics.semilogy(FREQ_0,AMPL_0); hold on; ma_graphics.semilogy(FREQ_i,AMPL_i); grid on xlabel('Frequency in Hz') ylabel('Amplitude in m/N') legend('Stiff coupling','Isolation','Location','SouthWest') xlim([5 50]) % display operation range fu_min = 13; fu_max = 33; rectangle('Position',[fu_min,1e-6,fu_max-fu_min,1.9e-4],'FaceColor',[0 .5 .5 0.2],'EdgeColor','b', 'LineWidth',1); % push rectangle (last plot) to the back h = get(gca,'Children'); set(gca,'Children',[h(2:end)',h(1)]); text(14,1.5e-6,'Operation range')
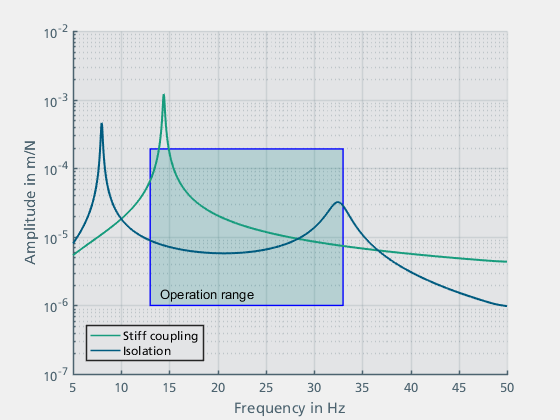
Abbildung 12: Ergebnisse im Frequenzbereich
Im nächsten Abschnitt wird untersucht, inwieweit die auftretenden Resonanzen durch den Einsatz eines Schwingungstilgers reduziert werden können.
Zunächst wird jedoch die Klasse ma_mosys der ma_Toolbox verwendet, um die Simulationsergebnisse analytisch nachzuvollziehen.
Analytische Lösung mit Hilfe der ma_mosys Klasse
Die Klasse ma_mosys kann verwendet werden um Mehrmassenschwinger aufzubauen und die Schwingungseigenschaften des Systems zu analysieren.
Hierfür wird zunächst ein Objekt der Klasse mit den entsprechenden Systemmatrizen (jData, kData) erstellt. Anschließend wird das System in den Zustandsraum (State-Space Modell) überführt und die Eigenwerte berechnet.
▾ Show source code
% Define the mass matrix of the system, where the first entry defines the mass annotation jData = [1 m_s; 2 m_m]; % Define arrangement of the masses and the spring and damper values of the respective connections kData = [1 inf k_s d_s; 1 2 k_i d_i]; % Force application points of the system originFvalue = 2; % Output velocity masses of the system outputPvalue = 1; system = ma_mosys(jData,kData,'originF',originFvalue,'outputP',outputPvalue); % Create the state-space model system.getSS; % Use the matlab built-in function eig to calculate the eigen values eigenValues = eig(system.SS); eigenFrq_i = unique(abs(eigenValues))/(2*pi);
Die analytisch berechneten Frequenzen 7.9778 Hz und 32.541 Hz decken sich mit den Ergebnissen aus Simulink. Für einen Abgleich des Amplitudengangs werden in Abbildung 13 die Transferfunktionen gegenübergestellt:
▾ Show source code
freq_analytic=0:0.1:50; [mag_analytic, phase_analytic]=bode(system.SS,freq_analytic*2*pi); mag_analytic = reshape(mag_analytic,1,length(freq_analytic)); h = figure(); ma_graphics.semilogy(FREQ_i,AMPL_i); hold on; ma_graphics.semilogy(freq_analytic,mag_analytic); hold off; grid on xlabel('Frequency in Hz') ylabel('Amplitude in m/N') legend('Simulink','Analytic','Location','SouthWest') xlim([5 50])
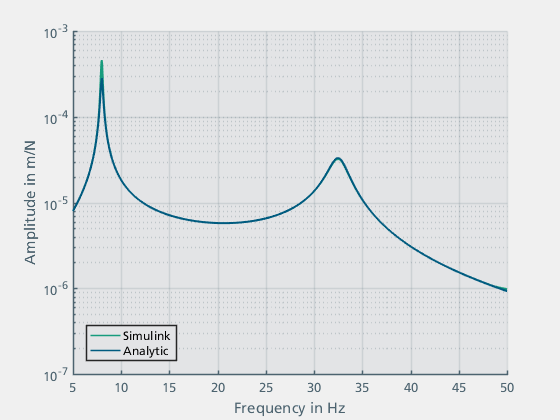
Abbildung 13: Abgleich des Simulink-Modells mit der analytischen Lösung
Es ist deutlich zu erkennen, dass die Ergebnisse aus der Simulation in Simulink und die Lösung des analytischen Modells übereinstimmen.
Vibrationsminderung durch einen Schwingungstilger
Es ist möglich, Vibrationen in einer Struktur durch zusätzliche strukturdynamische Maßnahmen, wie z. B. einen Schwingungstilger, zu reduzieren. Dabei wird die Amplitude einer strukturellen Resonanz reduziert. Die Vorgehensweise wird zunächst anhand des starr gelagerten Motors dargestellt. Dazu wird das in Abbildung 2 dargestellte Ersatzsystem um einen entsprechenden Tilger erweitert (siehe Abbildung 14). Im äquivalenten Feder-Dämpfer-System werden die Motormasse und der Tilger in der Position z = L/2 als überlagert angenommen.
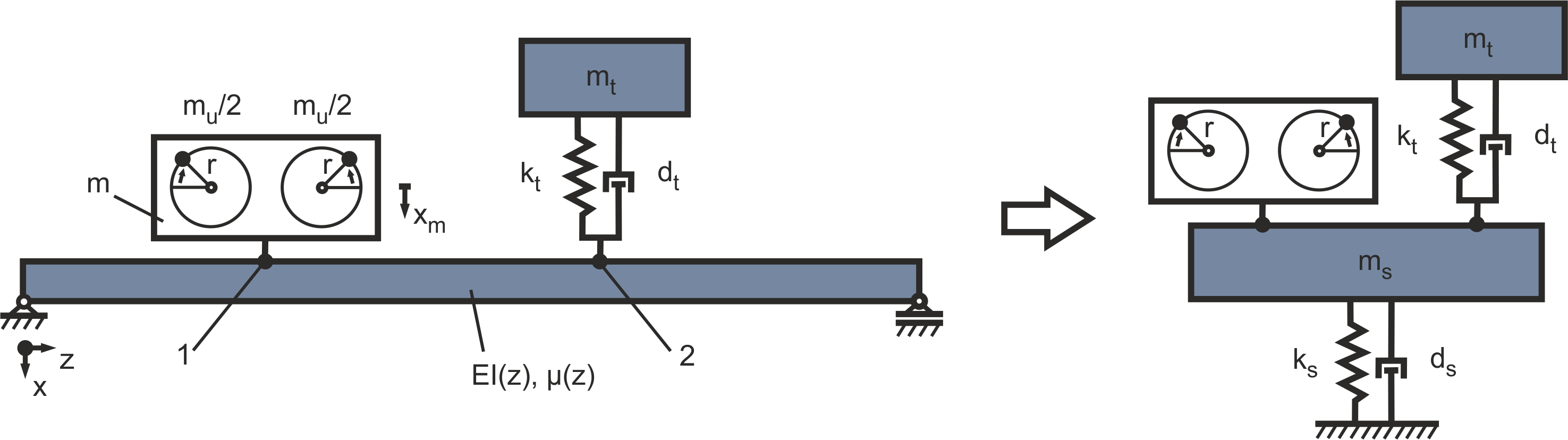
Abbildung 14: Starre Lagerung mit Tilger
Für einen effektiven Reduktionseffekt muss der Tilger auf die Eigenfrequenz der Struktur abgestimmt sein. Daher ist die geeignete Wahl der Parameter mt, kt entscheidend. Aber auch die Abstimmung der Dämpfung beeinflusst die Eigenschaften des Tilgers. Da eine analytische Optimierung der Parameter kompliziert ist, werden die Parameter abgeschätzt und die Qualität der Lösung anhand der graphischen Darstellung der Transmission bewertet und angepasst. Die Masse mt des Tilgers sollte zwischen 5% und 20% der Masse der Struktur (mges = mm + ms) betragen. Die Steifigkeit ist unter Berücksichtigung der dominierenden Resonanzfrequenz des starr gekoppelten Motors f1 = 14.411 Hz zu wählen. Daraus kann die Steifigkeit 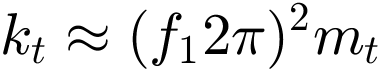 abgeschätzt werden. Der Dämpfungsgrad D sollte zwischen 5% und 20% liegen. Damit kann die Dämpfung dt zu
abgeschätzt werden. Der Dämpfungsgrad D sollte zwischen 5% und 20% liegen. Damit kann die Dämpfung dt zu 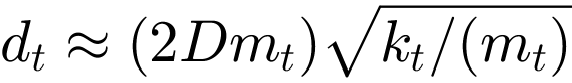 bestimmt werden.
bestimmt werden.
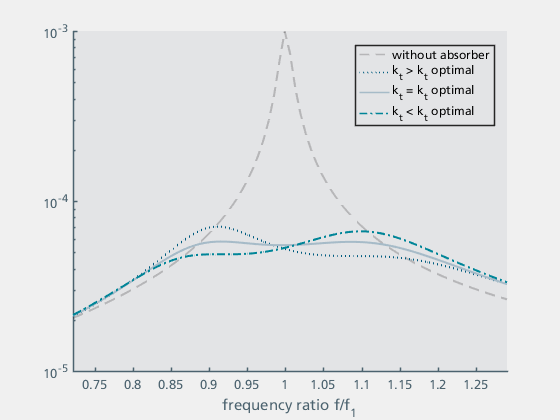
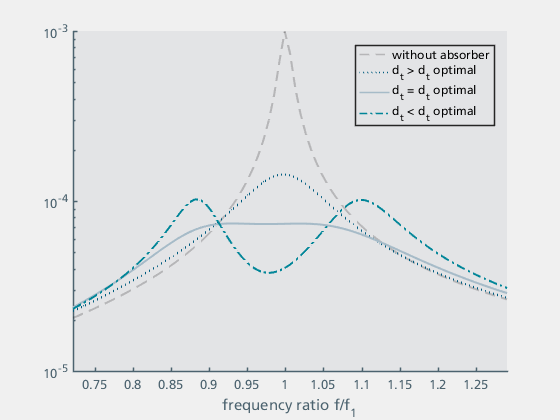
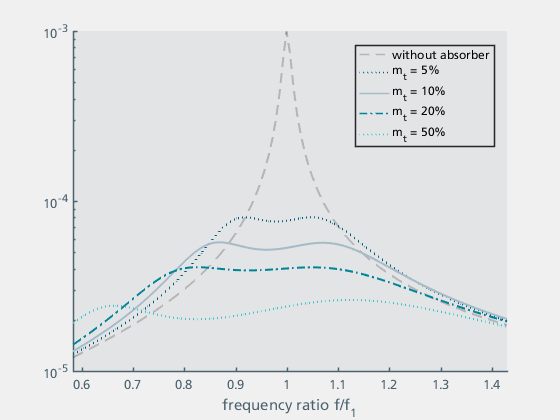
Bei der Parametrierung von Schwingungstilgern ist zu beachten, dass sich die Parameter mt, kt und dt gegenseitig beeinflussen. Zur Optimierung der Parameter empfielt sich daher ein iteratives Vorgehen. Der resultierende Kurvenverlauf gibt dabei Aufschluss über die Güte der Parameter. Abbildung 15 a – c zeigt den Einfluss der Parameter auf den Kurvenverlauf. Dabei wurde jeweils ein Parameter variiert, um den Einfluss auf den Kurvenverlauf darzustellen, während die beiden anderen Parameter angepasst wurden, um einen möglichst optimalen Verlauf zu erhalten. [3]
|
Abbildung 15a: Variation von kt |
Abbildung 15b: Variation von dt |
Abbildung 15c: Variation von mt |
| Abbildung 15a zeigt den Einfluss der Steifigkeit kt. Zum Vergleich ist auch der Fall ohne Tilger dargestellt. Die Steifigkeit kt und die Masse mt bestimmen die Tilgerfrequenz ft. Die Kurven der Struktur mit Tilger zeigen zwei Hügel, die bei optimaler Frequenz gleich hoch sind. Die Hügel liegen unterhalb und oberhalb der Eigenfrequenz der Struktur. Ist die Tilgerfrequenz zu niedrig (bzw. die Steifigkeit zu gering), ist der obere Hügel zu hoch, ist die Tilgerfrequenz zu hoch (bzw. die Steifigkeit zu groß), ist der untere Hügel zu hoch. | Abbildung 15b zeigt die Kurven für verschiedene Tilgerdämpfungen dt. Bei zu geringer Dämpfung werden beide Hügel zu hoch, bei zu hoher Dämpfung bleibt nur ein Hügel in der Mitte, der ebenfalls zu hoch ist. | Abbildung 15c sind die Kurven für verschiedene Verhältnisse von Tilgermasse mt zur Tragwerksmasse (mges). Es ist zu erkennen, dass die Dämpfungswirkung mit zunehmender Tilgermasse zunimmt und gleichzeitig der Kurvenverlauf breiter wird. In der Praxis gehen höhere Tilgermassen mit höheren Herstellungs- und Montagekosten des Schwingungstilgers sowie mit zusätzlichen statischen Lasten einher. Aus diesem Grund wird üblicherweise als Kompromiss eine Tilgermasse zwischen 5% und 20% gewählt. |
Implementierung in Simulink
Zur Simulation des Tilgers wurde das Simulinkmodel aus Abbildung 4 um eine Tilgermasse sowie ein Feder-Dämpfer-Element erweitert (siehe Abbildung 16).

Abbildung 16: Simulink Model des starr gelagerten Motors mit Tilger
Es wurde eine Tilgermasse mt von 100 kg angenommen. Dies entspricht einem Massenverhältnis mt/mges von ca. 12 %. Die Steifigkeit kt wurde in einem ersten Schritt mit 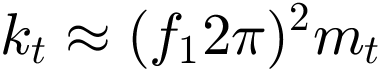 abgeschätzt. Dies ergibt einen Wert von 8.1984e+05 N/m. Als Dämpfungskonstante des Tilgers wurden die Werte 905.45 kg*s und 3621.8 kg*s verwendet. Dies entspricht einem Dämpfungsfaktor von 5% bzw. 20%. Zusätzlich wurde die Simulation mit einem iterativ optimierten Wert für kt_opti = 688660 N/m durchgeführt. Hierbei wurde ein Dämpfungsfaktor von 20% verwendet, was einer Dämpfungskonstante von 3319.4 kg*s entspricht. In Abbildung 17 sind die verschiedenen Simulationsergebnisse mit den Ergebnissen des starr gelagerten Motors ohne Tilger im Frequenzbereich gegenübergestellt.
abgeschätzt. Dies ergibt einen Wert von 8.1984e+05 N/m. Als Dämpfungskonstante des Tilgers wurden die Werte 905.45 kg*s und 3621.8 kg*s verwendet. Dies entspricht einem Dämpfungsfaktor von 5% bzw. 20%. Zusätzlich wurde die Simulation mit einem iterativ optimierten Wert für kt_opti = 688660 N/m durchgeführt. Hierbei wurde ein Dämpfungsfaktor von 20% verwendet, was einer Dämpfungskonstante von 3319.4 kg*s entspricht. In Abbildung 17 sind die verschiedenen Simulationsergebnisse mit den Ergebnissen des starr gelagerten Motors ohne Tilger im Frequenzbereich gegenübergestellt.
▾ Show source code
% Display simulation data in time domain simout_label = {'d_t = 5%','d_t = 20%','Iteratively optimised'}; [FREQ_0,AMPL_0,PHAS_0]=ma_frequency_response(time_0, F_0, x_0,{0,50},'window',true); h = figure(); ma_graphics.semilogy(FREQ_0,AMPL_0); hold on; for ind = 1:3 [FREQ_t(:,ind),AMPL_t(:,ind),PHAS_t(:,ind)]=ma_frequency_response(time_t(:,ind), F_t(:,ind), x_t(:,ind),{0,50},'window',true); ma_graphics.semilogy(FREQ_t(:,ind),AMPL_t(:,ind)); grid on xlabel('Frequency in Hz') ylabel('Amplitude in m/N') end legend('Stiff coupling',simout_label{:},'Location','best') xlim([5 50]) a=rectangle('Position',[f_u_min,1e-6,f_u_max-f_u_min,1.9e-4],'FaceColor',[0 .5 .5 0.2],'EdgeColor','b', 'LineWidth',1); % push rectangle (last plot) to the back ah = get(gca,'Children'); set(gca,'Children',[ah(2:end)',ah(1)]); text(14,1.5e-6,'Operation range')
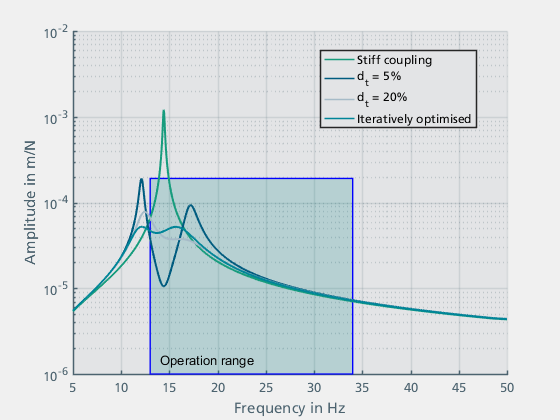
Abbildung 17: Ergebnisse der Reduktionswirkung durch einen Tilger mit einem Dämpfungsfaktor von 5% und 20% sowie einem iterativ optimierten Wert für kt
Für das leicht gedämpfte System wird die Resonanz gedämpft, wobei zwei Nachbarresonanzen entstehen. Diese resultieren aus dem zusätzlich in das System eingebrachten Freiheitsgrad. Bei der höheren Dämpfung ist die Amplitude der Nachbarresonanzen kleiner, wobei auch die Effizienz der Reduktionswirkung abnimmt. Der Verlauf bei dem iterativ optimierten Parameter kt ist nahezu linear. Da die erste Resonanzfrequenz des Tilgers außerhalb des Betriebsbereichs liegt, wäre es im vorliegenden Fall auch möglich, die Parameter kt und dt so zu optimieren, dass die Amplitude der zweiten Resonanzfrequenz möglichst klein wird.
Vergleich mit der analytischen Lösung
Für einen Vergleich der Simulationsergebnisse mit der analytischen Lösung werden die Systemmatrizen der iterativ optimierten Werte mit der ma_mosys Klasse abgeleitet und den Simulationsergebnissen gegenübergestellt.
▾ Show source code
% Define the mass matrix of the system, where the first entry defines the mass annotation jData = [1 m_s+m_m; 2 m_t]; % Define arrangement of the masses and the spring and damper values of the respective connections kData = [1 inf k_s d_s; 1 2 k_t_opti d_t_opti]; % Force application points of the system originFvalue = 1; % Output velocity masses of the system outputPvalue = 1; system = ma_mosys(jData,kData,'originF',originFvalue,'outputP',outputPvalue); % Create the state-space model system.getSS; % Use the matlab built-in function eig to calculate the eigen values eigenValues = eig(system.SS); eigenFrq_t = unique(abs(eigenValues))/(2*pi); freq_analytic=0:0.1:50; [mag_analytic, phase_analytic]=bode(system.SS,freq_analytic*2*pi); mag_analytic = reshape(mag_analytic,1,length(freq_analytic)); h = figure(); ma_graphics.semilogy(FREQ_t(:,3),AMPL_t(:,3)); hold on; ma_graphics.semilogy(freq_analytic,mag_analytic); hold off; grid on xlabel('Frequency in Hz') ylabel('Amplitude in m/N') legend('Simulink','Analytic') xlim([5 50])
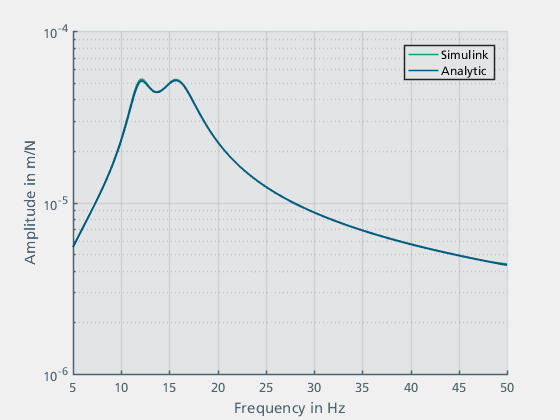
Abbildung 18: Abgleich des Simulink-Modells mit der Analytischen Lösung
Abbildung 18 zeigt, dass die Ergebnisse der Simulation und die Lösung des analytischen Modells übereinstimmen. Auch die berechneten Eigenfrequenzen 11.985 Hz und 15.88 Hz stimmen mit den beobachteten Resonanzfrequenzen überein.
Kombination der Schwingungsisolation mit einem Tilger
In den vorangegangenen Abschnitten wurden die Schwingungsisolierung und der Einsatz eines Schwingungstilgers getrennt betrachtet. Um eine optimale Schwingungsminderung zu erreichen, werden im Folgenden beide strukturdynamischen Maßnahmen kombiniert (Abbildung 19).
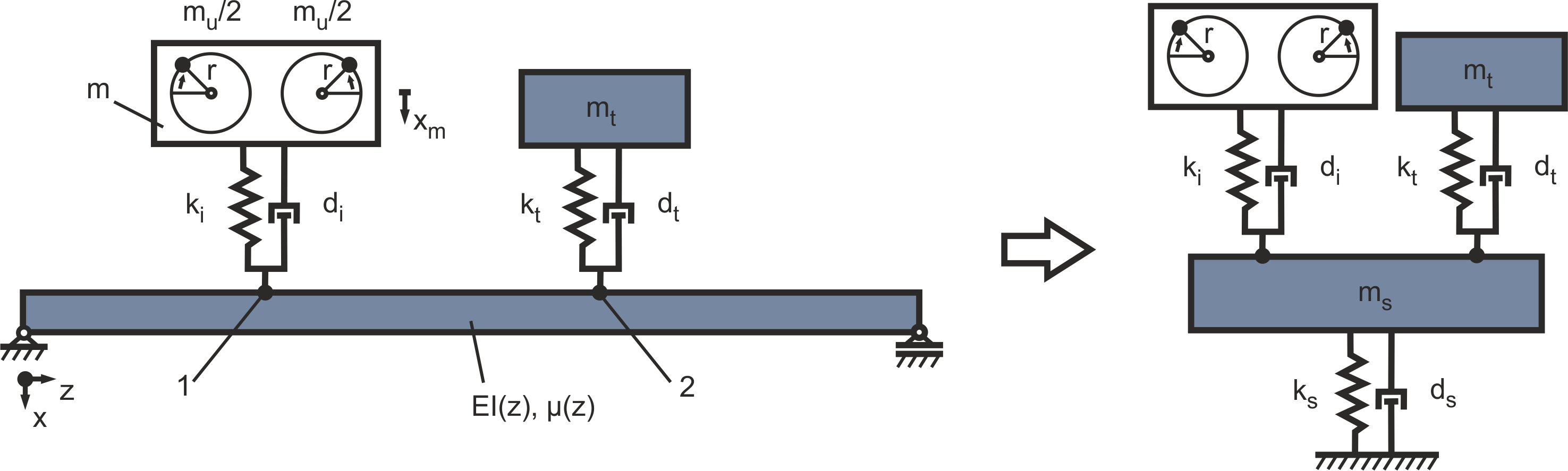
Abbildung 19: Elastische Lagerung mit Schwingungstilger
Zunächst müssen die Feder- und Dämpfungswerte des Tilgers an die Resonanzfrequenz des elastisch gelagerten Motors angepasst werden (siehe Abschnitt: Passive Isolation durch elastische Lagerstellen). Die Masse des Tilgers wird wiederum mit mt = 100 kg angenommen. Da in diesem Fall nur die Masse des Motors berücksichtigt wird entspricht dies einem Massenverhältnis von 17%. Ausgehend von der im Betriebsbereich vorherrschenden Resonanzfrequenz von 32.541 Hz wird der Wert für kt zunächst mit 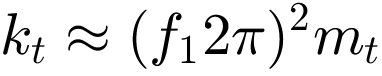 auf 4.1803e+06 N/m abgeschätzt. Daraus ergibt sich für die Dämpfungskonstante dt bei einem Dämpfungsfaktor von 5% ein Wert von 2044.6 kg*s und bei 20% Dämpfung ein Wert von zu 8178.3 kg*s. Auch hier wurden die Werte für kt und dt anschließend iterativ optimiert und zu 2090200 N/m und 7228.8 kg*s bestimmt.
auf 4.1803e+06 N/m abgeschätzt. Daraus ergibt sich für die Dämpfungskonstante dt bei einem Dämpfungsfaktor von 5% ein Wert von 2044.6 kg*s und bei 20% Dämpfung ein Wert von zu 8178.3 kg*s. Auch hier wurden die Werte für kt und dt anschließend iterativ optimiert und zu 2090200 N/m und 7228.8 kg*s bestimmt.
Abbildung 20 zeigt das Simulinkmodell des elastisch gelagerten Motors mit Schwingungstilger.

Abbildung 20: Simulink Model des elastisch gelagerten Motors mit Schwingungstilger
Abbildung 21 zeigt die Simulationsergebnisse mit einem Dämpfungsfaktor von 5% und 20% sowie das Ergebnis der iterativ optimierten Parameterwerte.
▾ Show source code
simout_label = {'d_t_i = 5%','d_t_i = 20%','Iteratively optimised'};
h = figure();
ma_graphics.semilogy(FREQ_0,AMPL_0);
hold on;
for ind = 1:3
[FREQ_t_i(:,ind),AMPL_t_i(:,ind),PHAS_t_i(:,ind)]=ma_frequency_response(time_t_i(:,ind), F_t_i(:,ind), x_t_i(:,ind),{0,50},'window',true);
ma_graphics.semilogy(FREQ_t_i(:,ind),AMPL_t_i(:,ind));
end
legend('Stiff coupling',simout_label{:},'Location','best')
xlim([5 50])
rectangle('Position',[f_u_min,1e-6,f_u_max-f_u_min,1.9e-4],'FaceColor',[0 .5 .5 0.2],'EdgeColor','b', 'LineWidth',1);
% push rectangle (last plot) to the back
hc = get(gca,'Children');
set(gca,'Children',[hc(2:end)',hc(1)]);
text(14,1.5e-6,'Operation range')
grid on;
xlabel('Frequency in Hz')
ylabel('Amplitude in m/N')
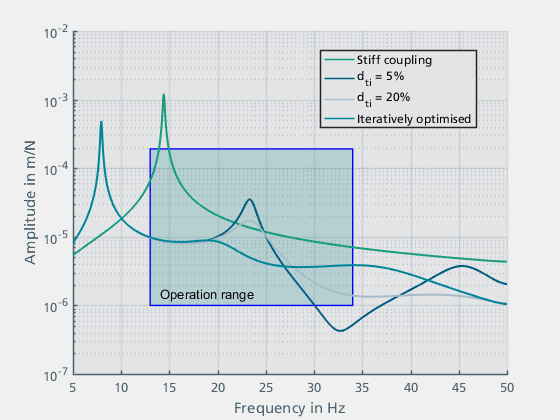
Abbildung 21: Simulationsergebnisse des elastisch gelagerten Motors mit Schwingungstilger
In diesem Tutorial wurde gezeigt wie unerwünschte Schwingungen durch strukturdynamische Maßnahmen reduziert werden können. Anhand des Modells eines Verbrennungsmotors in einem Schiff wurde der Einfluss einer elastischen Lagerung sowie eines Schwingungstilgers diskutiert und gezeigt wie das dynamische Verhalten mit Elementen der ma_Toolbox simuliert und bewertet werden kann.
In Abbildung 22 sind die Simulationsergebnisse der verschiedenen Maßnahmen gegenübergestellt. Durch eine elastische Lagerung des Motors wird eine Isolation der Anregung erreicht. Dadurch werden die in die Grundstruktur eingeleiteten Schwingungen deutlich reduziert. Es entsteht jedoch eine neue Resonanz im höheren Frequenzbereich, deren Amplitude in diesem Bereich größer ist als bei der starren Lagerung. Durch den Einsatz eines Schwingungstilgers ist es möglich, die Amplitude im Bereich der Eigenfrequenz der Grundstruktur deutlich zu reduzieren. In diesem Zusammenhang wurde der Einfluss der Steifigkeits- und Dämpfungsfaktoren des Tilgers diskutiert. Bei einem geringen Dämpfungsfaktor entstehen neue Resonanzfrequenzen, bei einem höheren Dämpfungsfaktor wird die Wirksamkeit des Tilgers deutlich reduziert. Die Kombination beider Maßnahmen führt über den gesamten Betriebsbereich zu den besten Ergebnissen. In diesem Fall wird der Schwingungstilger auf die Resonanzfrequenz ausgelegt, die sich durch die elastische Lagerung ergibt.
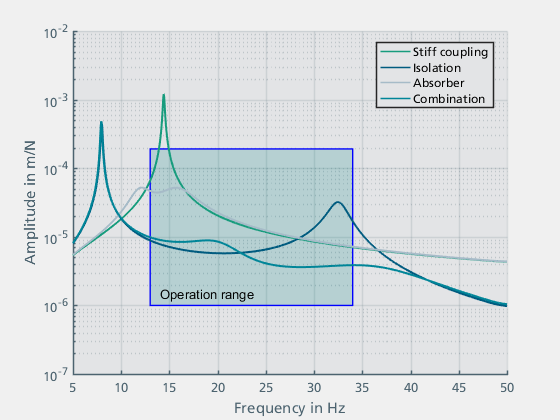
Abbildung 22: Gegenüberstellung der Reduktionswirkungen der verschiedenen Methoden
[1] Grote, K.-H.; Feldhusen, J. (Hg.) (2014): DUBBEL – Taschenbuch für den Maschinenbau, DOI: https://doi.org/10.1007/978-3-642-38891-0
[2] Böge, A.; Böge, W. (Hg.) (2021): Handbuch Maschinenbau – Grundlagen und Anwendungen der Maschinenbau-Technik, DOI: https://doi.org/10.1007/978-3-658-30273-3
[3] Weber, B. (2012): Tragwerksdynamik, DOI: https://doi.org/10.3929/ethz-a-007362062
[4] Preumont, A. (2011): Vibration Control of Active Structures – An Introduction, DOI: https://doi.org/10.1007/978-94-007-2033-6